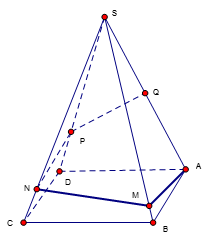
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên SA = 600 mét, góc \( \widehat {SAB} = {15^0}\) . Do có sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ A đến Q ngắn nhất. Tính tỉ số \( k = \frac{{AM + MN}}{{NP + PQ}}\)

Cho hình chóp (S.ABCD ) có đáy (ABCD ) là hình vuông cạnh bằng (3 ). Hai mặt phẳng  (SAB) và (SAC)  cùng vuông góc với mặt phẳng đáy. Góc giữa (SB ) và mặt phẳng đáy bằng 60⁰. Gọi (M ), (N ) là các điểm lần lượt thuộc cạnh đáy (BC ) và (CD ) sao cho (BM = 2MC ) và (CN = 2ND ). Tính khoảng cách giữa hai đường thẳng chéo nhau (DM ) và (SN. )

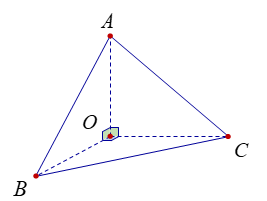
Xét tứ diện (OABC ) có (OA ), (OB ), (OC ) đôi một vuông góc. Gọi \(\alpha, \beta, \gamma \) lần lượt là góc giữa các đường thẳng (OA ), (OB ), (OC ) với mặt phẳng (ABC) (hình vẽ).

Khi đó giá trị nhỏ nhất của biểu thức \( M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)

Cho lăng trụ \(ABC.ABC\) các mặt đều là hình vuông cạnh a. Gọi D là trung điểm của cạnh \(BC.\) Tính khoảng cách giữa hai đường thẳng A’B’ và DC’ theo a

Cho lăng trụ đứng ABCA’B’C’có AC = a, BC= 2a, \(\widehat{ACB}={{120}^{o}}\). Đường thẳng A’C tạo với mặt phẳng (ABB’A’) góc 30⁰. Gọi M là trung điểm của BB’. Tính thể tích khối lăng trụ ABCA’B’C’ và khoảng cách giữa hai đường thẳng AM và CC’ theo a.

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh AB=a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60^o. Tính theo a thể tích tứ diện B’ABC và khoảng cách từ B đến mặt phẳng (AB’C).

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , mặt bên SAB  là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Gọi M là điểm thuộc SC sao cho MC=2MS. Biết AB=3, BC=\(3\sqrt{3}\). Khoảng cách giữa hai đường thẳng AC và BM là:

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác đều cạnh a. Góc giữa \(CA'\) và mặt \((AA'B'B)\) bằng \(30{}^\circ \). Gọi d(AI’,AC) là khoảng cách giữa \(A'I\) và AC, kết quả tính d(AI’,AC) theo a với I là trung điểm AB là

Cho lăng trụ tam giác \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) có tất cả các cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30⁰. Hình chiếu H của điểm A lên mặt phẳng \(\left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\) thuộc đường thẳng B₁C₁. Khoảng cách giữa hai đường thẳng AA₁ và BC₁ theo a là:  

Cho lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông, \(AB=BC=1,AA'=\sqrt{2}\). M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM; B'C.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), gọi M là điểm thuộc cạnh SC sao cho \(MC=2MS\). Biết \(AB=3,BC=3\sqrt{3}\), tính khoảng cách giữa hai đường thẳng AC và BM.

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(S\text{D}=\frac{a\sqrt{17}}{2}\) hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn \(AB.\) Gọi K là trung điểm của \(AD.\) Tính khoảng cách giữa hai đường SD và HK theo a?

Chóp tứ giác đều \(S.ABCD\) cạnh đáy bằng a, mặt bên tạo với mặt đáy góc \({{45}^{0}}\) . Ta có khoảng cách giữa hai đường thẳng AB và SC bằng:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\). Cạnh bên \(SA\) vuông góc với đáy, góc \(\widehat{SBD}={{60}^{0}}\). Tính theo \(a\) khoảng cách giữa hai đường thẳng \(AB\) và \(SO\).

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm H của cạnh AB. Góc tạo bởi SC và (ABCD) bằng 45⁰. Tính theo a tính khoảng cách giữa hai đường thẳng SD và AB.

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng \(a\sqrt{3};\widehat{ABC}={{120}^{0}}\) và cạnh bên SA vuông góc với mặt phẳng đáy. Biết rằng số đo của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60⁰. Khoảng cách giữa hai đường thẳng BD và SC bằng:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA=a\) và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC

Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a, \(\widehat{BAD}={{120}^{0}}\) và \(AC'=a\sqrt{5}\). Khoảng cách giữa hai đường thẳng AB’ và BD là:

Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh \(a\) . Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là \(\frac{{{a}^{3}}\sqrt{3}}{4}\). Tính khoảng cách giữa hai đường thẳng AA’ và BC.

Cho lăng trụ tam giác \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) có tất cả các cạnh bằng a, góc tại bởi cạnh bên và mặt phẳng đáy bằng \({{30}^{0}}\). Hình chiếu H của điểm A trên mặt phẳng \(\left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\)thuộc đường thẳng \({{B}_{1}}{{C}_{1}}\). Khoảng cách giữa hai đường thẳng \(A{{A}_{1}}\) và \({{B}_{1}}{{C}_{1}}\) theo a bằng:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45⁰. Tính khoảng cách giữa hai đường thẳng SB, AC.

Cho hình chóp S.ABC có AS, AB, AC đôi một vuông góc với nhau, \(AB=a,AC=a\sqrt{2}\). Tính khoảng cách d từ đường thẳng SA đến BC

Cho lăng trụ đứng \(ABC.ABC\) có đáy ABC là tam giác vuông tại B với \(AB=4a,BC=3\text{a},AC=5\text{a}\), cạnh bên \(BB'=9\text{a}\). Gọi M là điểm thuộc BB’ sao cho BB' = 3B'M. Khoảng cách giữa B’C và AM là

Lăng trụ đứng \(ABCA'B'C'\) đáy tam giác vuông cân tại B, cạnh bên \(CC'=a\sqrt{3}\). Biết thể tích khối trụ bằng \(2\sqrt{3}{{a}^{3}}\). Khoảng cách hai đường thẳng AB và CC’ bằng

Cho lăng trụ \(ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) có đáy ABCD là hình chữ nhật. AB = a, AD = \(a\sqrt{3}\). Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm AC và \(BD.\) Góc giữa hai mặt phẳng (ADD₁A₁) và (ABCD) bằng 60⁰. Tính khoảng cách từ điểm B₁ đến mặt phẳng (A₁BD) theo a.

Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng \(\sqrt{2}a\). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\frac{4}{3}{{a}^{3}}\). Khoảng cách h từ B đến mặt phẳng (SCD) là:

Cho hàm số S.ABC có \(ASB=BSC=CSA={{60}^{0}},SA=3,SB=4,SC=5\). Tính khoảng cách từ C đến mặt phẳng (SAB).

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), góc giữa SB và mặt phẳng (ABC) bằng 60 độ. Tính theo a khoảng cách từ B đến mặt phẳng (SMN), với M, N lần lượt là trung điểm của AB và AC.

Cho hình lăng trụ ABC.A’B’C’, đáy ABC có \(AC=a\sqrt{3};BC=3a,\widehat{ACB}={{30}^{0}}\). Cạnh bên hợp với mặt phẳng đáy góc \({{60}^{0}}\) và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC=3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Khoảng cách từ B đến mặt phẳng (A’AC) là:

Cho lăng trụ đứng ABCD.A’B’C’D’, đáy ABCD là hình chữ nhật có \(AB=a,AD=a\sqrt{3}\). Biết góc giữa đường thẳng A’C và mặt phẳng (ABCD) bằng \({{60}^{0}}\). Khoảng cách giữa đường thẳng B’C và C’D theo \(\alpha \) là:

Cho hình chóp tứ giác đều có độ dài cạnh bên và cạnh đáy cùng bằng a. Khi đó, khoảng cách h giữa đường thẳng AD và mặt phẳng (SBC) là:

Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB, SC tạo với đáy một góc \({{45}^{0}}\). Khoảng cách từ A đến mặt phẳng (SCD) là:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc \(BAC={{60}^{0}}\), hình chiếu của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABC, góc tạo bởi hai mặt phẳng (SAC) và (ABCD) là \({{60}^{0}}\). Tính khoảng cách từ B đến mặt phẳng (SCD) theo a.

Hình chóp có đáy là tam giác vuông tại B, BA = 3a, BC=4a, (SBC) vuông góc với đáy. Biết SB = 2a\(\sqrt3\), góc SBC = 30^o. Tính khoảng cách từ B đến (SAC)

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết \(BC=a\sqrt{3}\), \(BA=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S.ABC bằng\(\frac{{{a}^{3}}\sqrt{6}}{6}\). Khoảng cách h từ C đến mặt phẳng (SAB) là.

Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD với \(AB=2a,BC=a\). Các cạnh bên của hình chóp bằng nhau và bằng \(a\sqrt{2}\). Khoảng cách từ A đến mp (SCD) là:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(AB=1,AC=\sqrt{3}\). Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ B đến mặt phẳng (SAC).

Cho hình chóp S.ABCD có đáy ABCD là hình vuông \(BD=2a,\Delta SAC\) vuông tại S và nằm trong mặt phẳng vuông góc với đáy, \(SC=a\sqrt{3}\). Khoảng cách từ điểm B đến mặt phẳng (SAD) là:

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABD. Mặt bên SAB tạo với đáy một góc 60⁰. Tính theo a khoảng cách từ B đến mặt phẳng (SAD)?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(\widehat{ABC}={{30}^{0}}\), tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).

Cho lăng trụ \(ABCD.A'B'C'D'\) có đáy ABCD là hình chữ nhật. \(AB=a,AD=a\sqrt{3}\). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và \(BD.\) Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD) theo a là:

Cho hình chóp tứ giác đều S.ABCD, đáy có tất cả các cạnh bằng a và có tâm là O gọi M là trung điểm của OA. Tính khoảng cách d từ điểm M đến mặt phẳng (SCD).

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\), \(\widehat{D}={{60}^{0}}\)và \(SA\) vuông góc với \(\left( ABCD \right)\). Biết thể tích của khối chóp \(S.ABCD\) bằng \(\frac{{{a}^{3}}}{2}\). Tính khoảng cách \(k\) từ \(A\) đến mặt phẳng \(\left( SBC \right)\).

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB=a,\text{ }AC=a\sqrt{3}\). Tam giác \(SBC\) đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( SAC \right)\).

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt{3}\). SA vuông góc với đáy và SC = 3a. Khoảng cách từ điểm A đến mp(SCD) là:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến (SBD) bằng \(\frac{6a}{7}\) . Khoảng cách từ C đến mặt phẳng (SBD) bằng:

Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đá; \(BC=9m,AB=10m,AC=17m\). Biết thể tích khối chóp S.ABC bằng 73m³. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).

Cho hình chóp S.ABC có đáy ABC là tam giác cân, AB = BC = 2a, \(\widehat{ABC}={{120}^{0}}\), SA = 3a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).

Khối chóp S.ABC có đáy tam giác vuông cân tại B và \(AB=a.\,SA\bot \left( ABC \right)\). Góc giữa cạnh bên SB và mặt phẳng (ABC) bằng 60⁰. Khi đó khoảng cách từ A đến (SBC) là:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \({{a}^{3}}\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).