THÔNG TIN CHI TIẾT ĐỀ THI
Logo thi24h.vn
ĐỀ THI Toán học
Số câu hỏi: 50
Thời gian làm bài: 90 phút
Mã đề: #938
Lĩnh vực: Toán học
Nhóm: Toán 12 - Mũ và Logarit
Lệ phí: Miễn phí
Lượt thi: 4956

Ôn tập trắc nghiệm Hàm số lũy thừa Toán Lớp 12 Phần 4

Câu 1

Biểu thức T = log2 (ax2- 4x+1) có nghĩa với mọi x khi

A.
0 < a < 4 
B.
a > 0
C.
a > 4
D.
a ∈ ∅
Câu 2

Tìm tọa độ giao điểm của đồ thị hàm số y = 2- x+ 3  và đường thẳng y = 11.

A.
(3;11)
B.
(-3;11).
C.
(4;11)
D.
(-4;11).
Câu 3

Có tất cả bao nhiêu số nguyên của a để biểu thức T = log20 (12- 3a2) có nghĩa?

A.
1
B.
3
C.
5
D.
7
Câu 4

Tính đạo hàm của số hàm số y = log2(2x + 1)

A.
\(y' = \frac{2}{{\left( {2x + 1} \right)}}\)
B.
\(y' = \frac{1}{{\left( {2x + 1} \right)}}\)
C.
\(y' = \frac{2}{{\left( {2x + 1} \right)\ln 2}}\)
D.
\(y' = \frac{1}{{\left( {2x + 1} \right)\ln 2}}\)
Câu 5

Phát biểu nào sau đây sai?

A.
Hai hàm số y = ax và y= logax (a > 1) có cùng tình đơn điệu trên TXĐ.
B.
Đồ thị hàm số y = ax (a > 0 ; a ≠ 1) luôn nằm trên trục hoành
C.
Đồ thị hàm số y = logax( a > 0 và a ≠ 1) luôn nằm bên phải trục tung
D.
Hai hàm số y = ax và y = logax (0 < a < 1) đều có đồ thị nằm phía trên trục hoành
Câu 6

Cho hàm số y = xex . Đẳng thức nào sau đây là đúng.

A.
y’’ = 2y’-y
B.
y’’ = y’- 2y
C.
y’’ = 2xy’- y
D.
y’’ = 2y’-xy
Câu 7

Đạo hàm của hàm số f(x) = log3( 3x+1) là:

A.
\(f'(x) = \frac{{{3^x}\ln 3}}{{{3^x} + 1}}\)
B.
\(f'(x)=\frac{{{3^x}}}{{{3^x} + 1}}\)\)
C.
\(f'(x) = \frac{{{3^x}{{\ln }^2}3}}{{{3^x} + 1}}\)
D.
\(f'(x) = \frac{{{3^x}\ln 9}}{{{3^x} + 1}}\)
Câu 8

Đạo hàm của hàm số \(y\; = \;{e^{{x^2}}}.\sin x\) là:

A.
\(y'=\;{e^{{x^2}}}\left( {2x\sin x - \cos x} \right)\)
B.
\(y'=\;{e^{{x^2}}}\left( {2x\sin x + \cos x} \right)\)
C.
\(y'=\;{e^{{x^2}}}\left( {\sin x - \cos x} \right)\)
D.
\(y'=\;{e^{{x^2}}}\left( {\sin x + \cos x} \right)\)
Câu 9

 Tính đạo hàm của số hàm số y = log2(2x+1) 

A.
\(y'=\frac{2}{{\left( {2x + 1} \right)}}\)
B.
\(y'=\frac{1}{{\left( {2x + 1} \right)}}\)
C.
\(y'=\frac{2}{{\left( {2x + 1} \right)\ln 2}}\)
D.
\(y'=\frac{1}{{\left( {2x + 1} \right)\ln 2}}\)
Câu 10

Đạo hàm của hàm số y= 3x.x3 là:

A.
y’ = (ln3x+3) .x23x
B.
y’ = (ln3+3) .x23x
C.
y’ = (xln3+3) .x33x
D.
y’ = (ln3x+1) .x33x
Câu 11

Tập xác định của hàm số \(y\; = \;\sqrt {1 - \log \left( {2x - 1} \right)} \) là:

A.
\(D = \left( {\frac{1}{2};\frac{{11}}{2}} \right)\)
B.
\(D = \left[ {\frac{1}{2};\frac{{11}}{2}} \right)\)
C.
\(D = \left( {\frac{1}{2}; + \infty } \right)\)
D.
\(D = \left( {\frac{1}{2};\frac{{11}}{2}} \right]\)
Câu 12

Tập xác định của hàm số \(y\; = \;\sqrt { - 2{x^2} + 5x - 2}  + \ln \frac{1}{{{x^2} - 1}}\) là:

A.
D = (1;2)
B.
D = [1;2]
C.
D = [1;2)
D.
D= (1; 2]
Câu 13

Tập xác định của hàm số \(y\; = \;{\log _x}\left( {{2^x} - 2} \right) + {\log _{\sqrt 2 }}\frac{1}{{3\; - \;{x^2}}}\) là: 

A.
\(D = \left[ {1;\sqrt 3 } \right]\)
B.
\(D = \left( {1;\sqrt 3 } \right)\)
C.
\(D = \left( { - \sqrt 3 ;\sqrt 3 } \right)\)
D.
\(D = \left( { - \sqrt 3 ;1} \right)\)
Câu 14

Tập xác định của hàm số \(y\; = \;\frac{1}{{{2^x} + 1}} + \;{\log _{\sqrt 2 }}\frac{1}{{4 - x}}\) là

A.
\(D = \left( { - \infty ;4} \right)\)
B.
\(D = \left( { - \infty ;4} \right)\backslash \left\{ 0 \right\}\)
C.
\(D = \left( { - \infty ;4} \right)\backslash \left\{ -1\right\}\)
D.
\(D = \left( {4; + \infty } \right)\)
Câu 15

Tập xác định của hàm số \(y\; = \;\sqrt {{3^x} - 1}  + {\log _{0,3}}\left( {4 - {x^2}} \right)\) là:

A.
D = (-2;2)
B.
D = [0;2)
C.
D = (-2;-2)
D.
D = [0;2]
Câu 16

Nhận xét nào sau đây là sai.

A.
Đồ thị hàm số y = (0,3) x nhận đường thẳng y = 0 là tiệm cận ngang.
B.
Đồ thị hàm số y = log0,3x nhận đường thẳng x = 0 là tiệm cận đứng
C.
Hàm số y = 0, 3x và y = log0,3 x có cùng tập giá trị
D.
Đồ thị hàm số y = 0,3x nằm trên trục hoành
Câu 17

Tập xác định của hàm số \(y\; = \;{3^{\sqrt {2x - 1} }} + \sqrt {4 - {x^2}} \) là:

A.
\(D = \left( {\frac{1}{2};2} \right)\)
B.
\(D = \left( {\frac{1}{2};2} \right]\)
C.
\(D = \left[ {\frac{1}{2};2} \right]\)
D.
\(D = \left[ {\frac{1}{2};2} \right)\)
Câu 18

Đồ thị hàm số trong hình bên là đồ thị hàm số nào trong các hàm số dưới đây

 

A.
y = log4x
B.
\({\left( {\frac{1}{4}} \right)^x}\)
C.
y = 4x 
D.
y = x3+ 3x
Câu 19

Lấy đối xứng đồ thị hàm số y = log5x qua trục hoành ta được đồ thị hàm số nào trong các hàm số sau:

A.
\(y\; = \;{\log _{\frac{1}{5}}}x\)
B.
y = 5x
C.
y = 5-x 
D.
y = log5( –x) 
Câu 20

Lấy đối xứng đồ thị hàm số y = 5x qua trục hoành ta được đồ thị hàm số nào trong các hàm số sau

A.
y = log5x
B.
\(y\; = \;{\log _{\frac{1}{5}}}x\)
C.
y = 5-x
D.
y = - 5x
Câu 21

Đồ thị hàm số nào sau đây nhận 2 trục tọa độ làm 2 tiệm cận:

A.
y = log3x
B.
\(y\; = \;{x^{\frac{1}{5}}}\)
C.
y = 2x
D.
y = x-5
Câu 22

Khẳng định nào trong các khẳng định sau là sai.

A.
Đồ thị hàm số y = log2x và  đều nhận đường tiệm cận đứng là đường thẳng x = 0.
B.
Đồ thị hàm số y = log2x và đối xứng qua trục hoành
C.
Hàm số y = log2x có tập xác định là D = (0; + ∞)
D.
Hàm số y = log2x nghịch biến trên khoảng (0; 1) và đồng biến trên khoảng (0; + ∞) 
Câu 23

Cho hàm số \(y\; = \;{\log _{\frac{\pi }{e}}}\left( {3x - 2} \right)\). Khẳng định nào sau đây là sai

A.
Đồ thị hàm số đã cho nhận đường thẳng x = 2/3 là tiệm cận đứng
B.
Hàm số đã cho đồng biến trên khoảng \(\left( {\frac{2}{3}; + \infty } \right)\)
C.
Tập giá trị của hàm số đã cho là (0;+∞)
D.
Đạo hàm của hàm số đã cho là \(y'\; = \;\frac{3}{{x(\ln \pi  - 1)}}\)
Câu 24

Tập xác định của hàm số \(y\; = \;\sqrt {{2^x}}  + {\log _3}\left( {{x^2} - 2x} \right)\) là:

A.
\(D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
B.
\(D = \left( {2; + \infty } \right)\)
C.
\(D = \left( { - \infty ;0} \right] \cup \left( {2; + \infty } \right)\)
D.
\(D = \left[ {2; + \infty } \right)\)
Câu 25

Đạo hàm của hàm số \(y\; = \;{\left( {5 - x} \right)^{\sqrt 3 }}\) tại điểm x = 4 là

A.
\(- \sqrt 3 \)
B.
\( \sqrt 3 \)
C.
1
D.
0
Câu 26

Đạo hàm của hàm số \(y\; = \;{\left( {x - 1} \right)^{\frac{1}{3}}}\) tại điểm x = 2 là

A.
\(\frac{1}{3}\)
B.
1
C.
3
D.
0
Câu 27

Tìm tất cả các giá trị thực của tham số m để hàm số y= log(x2- 2x- m+ 1) có tập xác định là R

A.
m ≥ 0.
B.
m < 0
C.
m ≤ 2.
D.
m > 2.
Câu 28

Tìm m để hàm số y= 2x+ 2017+ ln(x2- 2mx+ 4) có tập xác định D = R:

A.
m = 2
B.
m > 2
C.
\(\left[ \begin{array}{l} m < 2\\ m >  - 2 \end{array} \right.\)
D.
\(\left\{ \begin{array}{l} m < 2\\ m >  - 2 \end{array} \right.\)
Câu 29

Cho x = 2000! . Giá trị của biểu thức \(A\; = \;\frac{1}{{{{\log }_2}x}} + \frac{1}{{{{\log }_3}x}} + ... + \frac{1}{{{{\log }_{2000}}x}}\) là:

A.
1
B.
- 1
C.
1000
D.
2000
Câu 30

Điều kiện xác định của biểu thức  \(T\; = \lg \sqrt {\left( {{x^2} - 4} \right)\left( {{x^2} - 6x + 9} \right)} \) là

A.
\(x \in \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\)
B.
x > 3
C.
\(x \in \left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\)
D.
\(x \in \left( { - \infty ; - 2} \right) \cup \left( {2;3} \right) \cup \left( {3; + \infty } \right)\)
Câu 31

Với giá trị nào của x thì biểu thức:  f(x) = log5( x3-x2-2x) xác định?

A.
0 < x < 1.
B.
x > 1
C.
\(x \in \left( { - 1;0} \right) \cup \left( {2; + \infty } \right)\)
D.
\(x \in \left( { 0;2} \right) \cup \left( {4; + \infty } \right)\)
Câu 32

Với giá trị nào của x thì biểu thức: f( x) = log6( 2x- x2)  xác định?

A.
0 < x < 2.
B.
x > 2.
C.
-1 < x < 1.
D.
x < 3.
Câu 33

Với giá trị nào của x thì biểu thức \(A\; = \;{\log _{\frac{1}{2}}}\frac{{x - 1}}{{3 + x}}\) xác định?

A.
-3 ≤ x ≤ 1.
B.
\(x \in R\backslash \left[ { - 3;1} \right]\)
C.
\(x \in R\backslash \left( { - 3;1} \right)\)
D.
-3< x < 1.
Câu 34

Với giá trị nào của x thì biểu thức C = ln( 4- x2) xác định?

A.
-2 < x < 2
B.
-2 ≤ x ≤ 2.
C.
x > 2
D.
x < -2
Câu 35

Trong các biểu thức sau biểu thức nào không có nghĩa

A.
(-2016)0.
B.
( -2016)2016.
C.
0- 2016.
D.
( -2016) -2016 .
Câu 36

Với giá trị nào của thì đẳng thức \(\sqrt[4]{{{x^4}}} = \frac{1}{{\left| x \right|}}\) đúng

A.
x ≠ 0
B.
x ≥ 0
C.
x = ± 1
D.
Không có giá trị nào
Câu 37

Tìm biểu thức không có nghĩa trong các biểu thức sau:

A.
( -3) -4.
B.
( -3) -1/3.
C.
04.
D.
\({\left( {\frac{1}{{{2^{ - 3}}}}} \right)^0}\)
Câu 38

Tìm x để biểu thức \({\left( {{x^2} + x + 1} \right)^{ - \frac{2}{3}}}\) có nghĩa:

A.
R
B.
Không tồn tại x
C.
x > 1
D.
x khác 0
Câu 39

Tìm tập xác định D của hàm số \(y = {\left( {{x^2} - 6x + 8} \right)^{\sqrt 2 }}\)

A.
D = R
B.
D = [4; +∞) ∪ (-∞; 2]
C.
D = (4; +∞) ∪ (-∞; 2)
D.
D = [2; 4]
Câu 40

Tìm x để biểu thức (2x - 1)– 2  có nghĩa:

A.
\(x \ne \frac{1}{2}\)
B.
\(x > \frac{1}{2}\)
C.
\(\frac{1}{2} < x < 2\)
D.
x < 2
Câu 41

Tìm tập xác định D của hàm số y = ( x3 - 8) -100

A.
D = ( 2; + ∞)
B.
D = R \ {2}
C.
D = ( -∞; 2)
D.
D = R \ ( -2; 2)
Câu 42

Tìm tập xác định D của hàm số y = (x2 - 3x + 2)100 

A.
D = [1; 2]
B.
D = [2; +∞) ∪ (-∞; 1]
C.
D = R
D.
D = (1; 2)
Câu 43

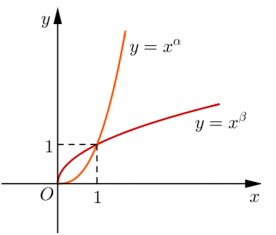
 Cho \(\alpha, \beta\) là các số thực. Đồ thị các hàm số \(y=x^{\alpha}, y=x^{\beta}\) , trên khoảng \((0 ;+\infty)\) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?

A.
\(0<\beta<1<\alpha\)
B.
\(\beta<0<1<\alpha\)
C.
\(0<\alpha<1<\beta\)
D.
\(\alpha<0<1<\beta\)
Câu 44

Cho hàm số \(y=x^{-\sqrt{2}}\) . Mệnh đề nào sau đây là sai?

A.
 Đồ thị hàm số không cắt trục hoành.
B.
Hàm số nghịch biến trên khoảng \((0 ;+\infty)\)
C.
Hàm số có tập xác định là \((0 ;+\infty)\)
D.
Đồ thị hàm số không có tiệm cận.
Câu 45

 Cho hàm số \(y=x^{e-3}\) trong các kết luận sau kết luận nào sai?

A.
Đồ thị hàm số nhận Ox, Oy làm hai tiệm cận.
B.
Đồ thị hàm số luôn đi qua M(1;1)
C.
Hàm số luôn đồng biến trên \((0,+\infty)\) 
D.
Tập xác định của hàm số là \(D=(0,+\infty)\)
Câu 46

 Cho hàm số\(y=x^{-\sqrt{2017}}\). Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số?

A.
Có một tiệm cận ngang và một tiệm cận đứng.
B.
Không có tiệm cận ngang và có một tiệm cận đứng.
C.
Có một tiệm cận ngang và không có tiệm cận đứng.
D.
Không có tiệm cận
Câu 47

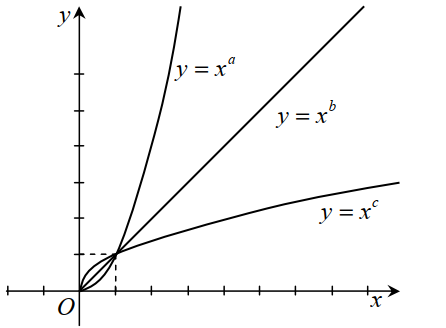
Hình vẽ bên là đồ thị các hàm số \(y=x^{a}, y=x^{b}, y=x^{c} \text { trên miền }(0 ;+\infty)\). Hỏi trong các số a , b , c số nào nhận giá trị trong khoảng  (0; 1) ?

A.
Số a
B.
Số a và c
C.
Số b
D.
Số c
Câu 48

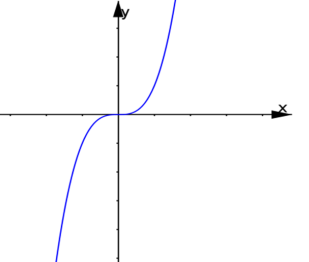
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?

A.
\(y=x^3\)
B.
\(y=x^4\)
C.
\(y=x^\frac{1}{5}\)
D.
\(y=\sqrt x\)
Câu 49

Cho hai số thực x , y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaaWcbeaakmaabmaabaGaam % iEaiabgUcaRiaadMhaaiaawIcacaGLPaaacqGHLjYScaaIXaaaaa!44A8! {\log _{{x^2} + {y^2}}}\left( {x + y} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức S = x+2y.

A.
3
B.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aI1aaaleqaaaaa!36CE! \sqrt 5 \)
C.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIZaGaey4kaSYaaOaaaeaacaaIXaGaaGimaaWcbeaaaOqaaiaaikda % aaaaaa!39F9! \frac{{3 + \sqrt {10} }}{2}\)
D.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aI1aGaey4kaSYaaOaaaeaacaaIXaGaaGimaaWcbeaaaOqaaiaaikda % aaaaaa!39FB! \frac{{5 + \sqrt {10} }}{2}\)
Câu 50

Cho hai số thực dương a,b thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbWaaW % baaSqabeaacaaIYaaaaOGaey4kaSIaamOyamaaCaaaleqabaGaaGOm % aaaakiabg6da+iaaigdaaaa!3EE1! {a^2} + {b^2} > 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGSbGaai % 4BaiaacEgadaWgaaWcbaGaamyyamaaCaaameqabaGaaGOmaaaaliab % gUcaRiaadkgadaahaaadbeqaaiaaikdaaaaaleqaaOWaaeWaaeaaca % WGHbGaey4kaSIaamOyaaGaayjkaiaawMcaaiabgwMiZkaaigdaaaa!46E1! {\log _{{a^2} + {b^2}}}\left( {a + b} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức P = 2a + 4b - 3.

A.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaam % aakaaabaGaaGymaiaaicdaaSqabaaakeaacaaIYaaaaaaa!3AF0! \frac{{\sqrt {10} }}{2}\)
B.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaGcaaqaai % aaigdacaaIWaaaleqaaaaa!3A1A! \sqrt {10} \)
C.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaai % aaikdadaGcaaqaaiaaigdacaaIWaaaleqaaaGcbaGaaGOmaaaaaaa!3BAC! \frac{{2\sqrt {10} }}{2}\)
D.
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaai % aaigdaaeaadaGcaaqaaiaaigdacaaIWaaaleqaaaaaaaa!3AE5! \frac{1}{{\sqrt {10} }}\)