Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;2) và B(3;4). Điểm \(P\left( {\frac{a}{b};0} \right)\) (với \(\frac a b\) là phân số tối giản) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b.

Đồ thị hàm số y = x - 2m + 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng \(\frac{{25}}{2}\). Khi đó m bằng

Các đường thẳng \(y = - 5\left( {x + 1} \right)\); y = 3x + a; y = ax + 3 đồng quy với giá trị của a là

Đường thẳng \(d:y = \left( {m - 3} \right)x - 2m + 1\) cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là

Cho hàm số \(y = \left( {m + 2} \right)x + \sqrt {2 - m} \). Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên R?

Đường thẳng \({d_m}:\left( {m - 2} \right)x + my = - 6\) luôn đi qua điểm:

Tìm điểm M(a;b) với a < 0 nằm trên \(\Delta :x + y - 1 = 0\) và cách N(-1;3) một khoảng bằng 5. Giá trị của a - b là

Một hộ nông dân định trồng đậu và cà trên diện tích 800m². Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên 100m² nếu trồng cà thì cần 30 công và thu 4 000 000 đồng trên 100 m² Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180. Hãy chọn phương án đúng nhất trong các phương án sau:

Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng \(P\left( n \right) = 360 - 10n\) (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lương cá sau một vụ thu được nhiều nhất?

Tìm các giá trị thực của tham số m để đường thẳng \(y = \left( {{m^2} - 3} \right)x + 3m + 1\) song song với đường thẳng y = x - 5?

Đồ thị hàm số y = ax + b cắt trục hoành tại điểm có hoành độ x = 3 và đi qua điểm M(-2;4). Giá trị a, b là:

Cho hai đường thẳng \(\left( {{d_1}} \right):y = \frac{1}{2}x + 100\) và \(\left( {{d_2}} \right):y = - \frac{1}{2}x + 100\). Mệnh đề nào sau đây đúng?

Cho hàm số bậc nhất \(y = \left( {{m^2} - 4m - 4} \right)x + 3m - 2\) có đồ thị là (d). Tìm số giá trị nguyên dương của m để đường thẳng (d) cắt trục hoành và trục tung lần lượt tại hai điểm A, B sao cho tam giác OAB là tam giác cân (O là gốc tọa độ).

Đồ thị của hàm số \(y = \frac{2}{3}x + \frac{1}{3}\) là

Điểm A có hoành độ x_A = 1 và thuộc đồ thị hàm số y = mx + 2m - 3. Tìm m để điểm A nằm trong nửa mặt phẳng tọa độ phía trên trục hoành (không chứa trục hoành).

Đường thẳng đi qua điểm M(2;-1) và vuông góc với đường thẳng \(y = - \frac{1}{3}x + 5\) có phương trình là

Đường thẳng y = ax + b có hệ số góc bằng 2 và đi qua điểm A(-3;1) là

Tìm m để hàm số \(y = \left( {3 - m} \right)x + 2\) nghịch biến trên R.

Cho hàm số y = ax + b có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?

Hàm số nào cho dưới đây có đồ thị như hình vẽ bên:

Biết ba đường thẳng \({d_1}:y = 2x - 1\), \({d_2}:y = 8 - x\), \({d_3}:y = \left( {3 - 2m} \right)x + 2\) đồng quy. Giá trị của m bằng

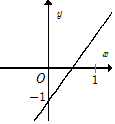
Hàm số y = 2x - 1 có đồ thị là hình nào trong các hình sau?

Hàm số \(f\left( x \right) = ax - \sqrt {1 - a} \) đồng biến trên R khi và chỉ khi

Đồ thị hàm số nào sau đây đi qua  điểm A(-1;2) và B(0;-1).

Hàm số \(y = \left( {m - 1} \right)x - \sqrt {2 - m} \) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\) khi:

Biết đồ thị hàm số y = ax + b đi qua điểm M(1;4) và có hệ số góc bằng -3. Tích P = ab?

Hàm số \(y = \left( {m - 1} \right)x - \sqrt {2 - m} \) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\) khi:

Biết đồ thị hàm số y = ax + b đi qua điểm M(1;4) và có hệ số góc bằng -3. Tích P = ab?

Tìm các giá trị của tham số m để hàm số \(y = \left( {2m + 3} \right)x + m + 3\) nghịch biến trên R

Cho hàm số \(f\left( x \right) = \left( {m - 2} \right)x + 1\). Với giá trị nào của m thì hàm số đồng biến trên R?; nghịch biến trên R?

Một hàm số bậc nhất y = f(x) có f(-1) = 2 và f(2) = -3. Hàm số đó là

Hàm số nào trong bốn phương án liệt kê ở A, B, C, D có đồ thị như hình bên:

Tìm điều kiện của tham số m để hàm số \(y = \left( {3m + 4} \right)x + 5m\) đồng biến trên R

Tìm m để hàm số \(y = \left( { - 2m + 1} \right)x + m - 3\) đồng biến trên R.

Tìm m để hàm số \(y = \left( {3 - m} \right)x + 2\) nghịch biến trên R.

Khẳng định nào về hàm số y = 3x + 5 là sai:

Đường thẳng nào sau đây song song với đường thẳng \(y = \sqrt 2 x\)

Đường thẳng nào sau đây song song với đường thẳng \(y = \sqrt 2 x\)

Hàm số \(f\left( x \right) = \left( {m - 1} \right)x + 2m + 2\) là hàm số bậc nhất khi và chỉ khi

Điểm nào sau đây thuộc đồ thị hàm số \(y = \left| {x + 2} \right| + \left| {3x - 1} \right| + \left| { - x + 4} \right|\) ?

Đường thẳng \(y = ax + b\) với đồ thị sau có phương trình là

Phương trình đường thẳng song song với đường thẳng \(y =  - 2x + 21\) và đi qua điểm \(P\left( {3;10} \right)\) là

Xác định các hệ số \(a\) và \(b\) để đồ thị của hàm số \(y = ax + b\) đi qua \(P(4;2)\) và \(Q\left( {1;1} \right)\).

Xác định các hệ số \(a\) và \(b\) để đồ thị của hàm số \(y = ax + b\) đi qua \(M( - 1; - 2)\) và \(N(99; - 2)\).

Xác định các hệ số \(a\) và \(b\) để đồ thị của hàm số \(y = ax + b\) đi qua \(A(\dfrac{2}{3}; - 2)\) và \(B\left( {0;1} \right)\)  

Cho hàm số \(y=x-|x|\) . Trên đồ thị của hàm số lấy hai điểm A và B có hoành độ lần lượt là –2 và 1 . Phương trình đường thẳng AB là

Phương trình đường thẳng y=a x+b đi qua hai điểm A(-1;2) và B(3;1) là

Hàm số \(y=|-x-3|+|2 x+1|+|x+1|\) đồng biến trong khoảng nào dưới đây?

Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?

Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?