
ĐỀ THI Toán học
Ôn tập trắc nghiệm Hàm số bậc hai Toán Lớp 10 Phần 2
Xác định phương trình của Parabol có đỉnh I(0;-1) và đi qua điểm A(2;3).
Parabol \(y = a{x^2} + bx + c\) đạt cực tiểu bằng 4 tại x = -2 và đồ thị đi qua A(0;6) có phương trình là
Hàm số \(y = - {x^2} + 2x - 5\) đồng biến trên khoảng:
Cho hàm số \(y = 2{x^2} - 4x + 3\) có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
Đồ thị hình bên dưới là đồ thị của hàm số nào?
.png)
Tìm parabol \(\left( P \right):y = a{x^2} + 3x - 2\), biết rằng parabol có trục đối xứng x = -3
Cho parabol (P) có phương trình \(y = 3{x^2} - 2x + 4\). Tìm trục đối xứng của parabol
Xác định a, b, c biết Parabol có đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua các điểm M(0;-1), N(1;-1), P(-1;1).
Đồ thị hàm số \(y = m{x^2} - 2mx - {m^2} - 2\) \(\left( {m \ne 0} \right)\) là parabol có đỉnh nằm trên đường thẳng y = x - 3 thì m nhận giá trị nằm trong khoảng nào dưới đây?
Hàm số \(y = {x^2} - 4x + 3\) đồng biến trên khoảng nào?
Biết đường thẳng d: y = mx cắt Parabol \(\left( P \right):y = {x^2} - x + 1\) tại hai điểm phân biệt A, B. Khi đó tọa độ trung điểm I của đoạn thẳng AB là
Đồ thị hình bên dưới là đồ thị của hàm số nào?

Cho đường thẳng d:y = x + 1 và Parabol \(\left( P \right):y = {x^2} - x - 2\). Biết rằng d cắt (P) tại hai điểm phân biệt A, B. Khi đó diện tích tam giác OAB (với O là gốc hệ trục tọa độ) bằng
Chọn mệnh đề sai trong các mệnh đề sau:
Hàm số \(y = - {x^2} + 6x + 5\) có
Cho parabol (P): \(y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng x = 1. Khi đó 4a + 2b bằng
Bảng biến thiên sau là của hàm số nào
Cho hàm số \(y = {x^2} - 4x - 5\). Trong các mệnh đề sau mệnh đề nào đúng.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-7;7] để phương trình \(m{x^2} - 2\left( {m + 2} \right)x + m - 1 = 0\) có hai nghiệm phân biệt?
Có bao nhiêu giá trị thực của m để đường thẳng d: y = 4x - 2m tiếp xúc với parabol \(\left( P \right):\,y = \left( {m - 2} \right){x^2} + 2mx - 3m + 1\)
Tìm giá trị nhỏ nhất của hàm số \(y = {x^2} - 4x + 1\).
Đồ thị của hàm số nào sau đây là parabol có đỉnh I(-1;3)
Xác định parabol (P): \(y = a{x^2} + bx + c\), a khác 0 biết (P) cắt trục tung tại điểm có tung độ bằng 1 và có giá trị nhỏ nhất bằng \(\frac34\) khi \(x = \frac{1}{2}\)
Câu 110.Xét tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2} - 4x + 5\) trên các khoảng \(\left( { - \infty ;\,2} \right)\) và \(\left( {2;\, + \infty } \right)\). Khẳng định nào sau đây đúng?
Giao điểm của parabol \(\left( P \right):y = {x^2} - 3x + 2\) với đường thẳng y = x - 1 là
Cho hàm số \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có đồ thị là parabol (P). Xét phương trình \(a{x^2} + bx + c\, = 0\) (1). Chọn khẳng định sai:
Một chiếc cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\). Biết cổng có chiều rộng d = 5 mét (như hình vẽ). Hãy tính chiều cao h của cổng.
.png)
Nghiệm của phương trình \({x^2}-8x + 5 = 0\) có thể xem là hoành độ giao điểm của hai đồ thị hàm số:
Cho hàm số (P): \(y = \left( {m - 1} \right){x^2} - 2\left( {m - 2} \right)x + m - 3\,\,\left( {m \ne 1} \right)\). Đỉnh của (P) là S(-1;-2) thì m bằng bao nhiêu:
Cho parabol \(\left( P \right):y = 3{x^2} - 2x + 1\). Điểm nào sau đây là đỉnh của (P)?
Tọa độ đỉnh I của parabol \(y = {x^2} - 2x + 7\) là
Trục đối xứng của parabol \(y = 2{x^2} + 2x - 1\) là đường thẳng có phương trình
Viết phương trình trục đối xứng của đồ thị hàm số \(y = {x^2} - 2x + 4\).
Parabol \(\left( P \right):y = - 2{x^2} - 6x + 3\) có hoành độ đỉnh là?
Cho hàm số: \(y = {x^2} - 2x - 1\), mệnh đề nào sai:
Bảng biến thiên nào dưới đây là của hàm số \(y = - {x^2} + 2x + 1\)
.png)
.png)
.png)
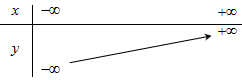
Parabol \(y = - {x^2} + 2x + 3\) có phương trình trục đối xứng là
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?

Phương trình \(a{x^2} + bx + c = 0{\rm{ }}\left( {a \ne 0} \right)\) có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
Cho hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a > 0} \right)\). Khẳng định nào sau đây là sai?
Cho hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) có đồ thị (P), đỉnh của (P) được xác định bởi công thức nào?
Trục đối xứng của parabol \(y = - {x^2} + 5x + 3\) là đường thẳng có phương trình
Xác định parabol \(y = a{x^2} + bx + c\) biết parabol đi qua hai điểm A(-1; 2), B(2; 3) và có trục đối xứng là đường thẳng x = 1.
Xác định parabol \(y = a{x^2} + bx + c\) biết parabol đi qua gốc tọa độ và có đỉnh là điểm (1;2).
Xác định parabol \(y = a{x^2} + bx + c\) biết parabol nhận trục tung làm trục đối xứng và cắt đường thẳng \(y = \dfrac{x}{2}\)tại các điểm có hoành độ là -1 và \(\dfrac{3}{2}\).
Giao điểm của parabol \(y = {x^2} + 4x - 6\) và đường thẳng \(y = 2x + 2\) là
Hàm số bậc hai \(y = a{x^2} - 2x + c\) có đồ thị với đỉnh \(I\left( {2; - 1} \right)\) là
Hàm số bậc hai \(y = a{x^2} + bx - 6\) có đồ thị đi qua hai điểm \(A\left( {1;1} \right)\) và \(B\left( {2;2} \right)\) là
Trục đối xứng của parabol \(y = \dfrac{1}{5}{x^2} + 2x + 7\) là
Tọa độ đỉnh của paranol \(y = - \dfrac{1}{2}{x^2} + 6x + 1\) là
