THÔNG TIN CHI TIẾT ĐỀ THI

ĐỀ THI Toán học
Số câu hỏi: 50
Thời gian làm bài: 90 phút
Mã đề: #5186
Lĩnh vực: Toán học
Nhóm: THI THPTQG
Lệ phí:
Miễn phí
Lượt thi: 1214
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Câu 1
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình sau?
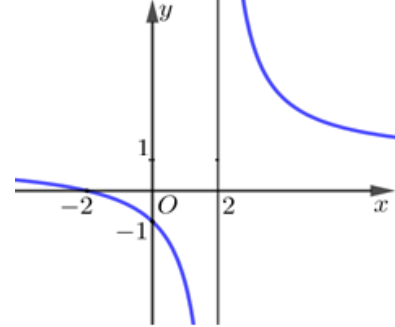

A.
\(y=\frac{x+2}{x-2}\)
B.
\(y=x^{3}+3 x^{2}-1\)
C.
\(y=-x^{4}+2 x^{2}-1\)
D.
\(y=\frac{x-2}{x+2}\)
Câu 2
Cho hình chóp S. ABC có \(S A=S B\,\, và \,\,C A=C B\) . Góc giữa hai đường thẳng SC và AB bằng
A.
\(90^{\circ}\)
B.
\(30^{\circ}\)
C.
\(45^{\circ}\)
D.
\(60^{\circ}\)
Câu 3
Giá trị lớn nhất của hàm số \(y=\frac{3 x-1}{x-3}\)-trên \([0 ; 2]\) là:
A.
\(\frac{-1}{3}\)
B.
\(\frac{1}{3}\)
C.
5
D.
-5
Câu 4
Số nghiệm của phương trình \(\log _{2}\left(x^{2}-x+2\right)=1\) là:
A.
1
B.
3
C.
0
D.
2
Câu 5
Cho lăng trụ đều ABC.A' B'C' có cạnh đáy bằng 2a, độ dài cạnh bên bằng \(a \sqrt{3}\) . Tính thể tích V của khối lăng trụ
A.
\(V=a^{3}\)
B.
\(V=\frac{1}{4} a^{3}\)
C.
\(V=\frac{3}{4} a^{3}\)
D.
\(V=3 a^{3}\)
Câu 6
Cho a là số thực dương khác 1 . Tính \(I=\log _{\sqrt{a}} a\)
A.
\(I=-\frac{1}{2}\)
B.
\(I=\frac{1}{2}\)
C.
I=-2
D.
I=2
Câu 7
Tính thể tích V của khối chóp có đáy là hình vuông cạnh bằng 3 và chiều cao bằng 4
A.
V=16
B.
V=12
C.
V=9
D.
V=48
Câu 8
Hàm số \(y=x^{4}-2 x^{2}+1\)nghịch biến trên khoảng nào sau đây?
A.
\((-\infty ; 1)\)
B.
\((-1 ; 0)\)
C.
\((-1 ; 1)\)
D.
\((-\infty ;-1)\)
Câu 9
Thể tích khối cầu có bán kính r bằng
A.
\(\frac{4}{3} \pi r^{2}\)
B.
\(\frac{2}{3} \pi r^{3}\)
C.
\(V=4 \pi r^{3}\)
D.
\(\frac{4}{3} \pi r^{3}\)
Câu 10
Cho số phức \(z=2-3 i\) . Phần ảo của số phức z là.
A.
\(-3 i\)
B.
2
C.
-3
D.
3
Câu 11
Xét số phức z thỏa mãn \((\bar{z}+2 i)(z-2)\)là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biễu diễn các số phức z là một đường tròn có tâm là điểm nào dưới đây?
A.
\(Q(2 ; 2)\)
B.
\(M(1 ; 1)\)
C.
\(P(-2 ;-2)\)
D.
\(N(-1 ;-1)\)
Câu 12
Nếu \(\int\limits_{1}^{2} f(x) d x=5 \text { và } \int\limits_{1}^{2} g(x) d x=-7 \text { thì } \int\limits_{1}^{2}(2 f(x)+g(x)) d x\) bằng
A.
-3
B.
-1
C.
3
D.
1
Câu 13
Họ tất cả các nguyên hàm của hàm số \(f(x)=3 x^{2}+\frac{1}{x}\) là:
A.
\(x^{3}+\ln x+C\)
B.
\(x^{3}+\ln |x|+C\)
C.
\(x^{3}-\frac{1}{x^{2}}+C\)
D.
\(6 x+\ln |x|+C\)
Câu 14
Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức \(z=3+4 i\) là điểm nào dưới dây?
A.
\(Q(-4 ; 3)\)
B.
\(N(3 ;-4)\)
C.
\(M(-4 ;-3)\)
D.
\(P(3 ; 4)\)
Câu 15
Tính diện tích xung quanh của hình nón có bán kính đáy \(r=\sqrt{3}\) và chiều cao h = 4
A.
\(S_{x q}=2 \sqrt{57} \pi\)
B.
\(S_{x q}=8 \sqrt{3} \pi\)
C.
\(S_{x q}=4 \sqrt{3} \pi\)
D.
\(S_{x q}=\sqrt{57} \pi\)
Câu 16
Quay hình vuông ABCD cạnh a xung quanh một cạnh .Thể tích khối trụ được tạo thành là:
A.
\(\frac{1}{3} \pi a^{3}\)
B.
\(3 \pi a^{3}\)
C.
\(2 \pi a^{3}\)
D.
\(\pi a^{3}\)
Câu 17
Cho cấp số nhân \((u_n )\) có \(u_{2}=\frac{1}{4} \text { và } u_{3}=1\). Tìm công bội q
A.
\(q=-\frac{1}{2}\)
B.
\(q=-4\)
C.
\(q=\frac{1}{2}\)
D.
\(q=4\)
Câu 18
Trong không gian Oxyz , cho đường thẳng \(d: \frac{x-1}{2}=\frac{y+1}{1}=\frac{z-1}{2}\). Véc tơ nào sau đâu là véc tơ chỉ phương của đường thẳng d
A.
\(\vec{u}=(2 ; 1 ; 2)\)
B.
\(\vec{u}=(-2 ; 1 ; 1)\)
C.
\(\vec{u}=(1 ;-1 ; 1)\)
D.
\(\vec{u}=\left(-\frac{1}{2} ; 1 ; \frac{1}{2}\right)\)
Câu 19
Cho số phức \(z=2+i . \operatorname{Tính }|z|\)
A.
3
B.
\(\sqrt{3}\)
C.
2
D.
\(\sqrt{5}\)
Câu 20
Có bao nhiêu cách để 10 người ngồi vào 10 ghế xếp thành hàng dài sao cho mỗi người ngồi đúng một ghế ?
A.
\(\frac{1}{10}\)
B.
\(C_{10}^{10}\)
C.
\(10^{10}\)
D.
\(10 !\)
Câu 21
Tập nghiệm của bất phương trình \(e^{x^{2}-x+1}<e\)
A.
\((0 ; 1)\)
B.
\((1 ; 2)\)
C.
\((1 ;+\infty)\)
D.
\((-\infty ; 0)\)
Câu 22
Tổng số đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x-1}{x+1}\)
A.
0
B.
1
C.
3
D.
2
Câu 23
Tìm tập xác định D của hàm số \(y=(2-x)^{\frac{1}{3}}\)
A.
\(D=(-\infty ; 2]\)
B.
\(D=(-\infty ;+\infty) .\)
C.
\(D=(-\infty ; 2)\)
D.
\(D=(2 ;+\infty)\)
Câu 24
Cho lăng trụ tam giác đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có độ dài cạnh đáy bằng a, góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng \(60^{\circ} .\) . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho
A.
\(V=\frac{a^{3} \pi \sqrt{3}}{3}\)
B.
\(V=\frac{a^{3} \pi \sqrt{3}}{9}\)
C.
\(V=a^{3} \pi \sqrt{3}\)
D.
\(V=\frac{4 a^{3} \pi \sqrt{3}}{3}\)
Câu 25
Cho \(a=\log _{2} 5, b=\log _{2} 9\). Biểu diễn của \(P=\log _{2} \frac{40}{3}\) theo a và b là
A.
\(P=3+a-\sqrt{b}\)
B.
\(P=3+a-2 b\)
C.
\(P=3+a-\frac{1}{2} b\)
D.
\(P=\frac{3 a}{2 b}\)
Câu 26
Tính thể tích vật thể giới hạn bởi các mặt phẳng x =0 và x= 1, biết thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoàng độ \(0 \leq x \leq 1\) là một hình vuông có độ dài cạnh \(\sqrt{x (e^{x}-1)}\).
A.
\(V=\frac{\pi}{2}\)
B.
\(V=\frac{1}{2}\)
C.
\(V=\frac{e-1}{2}\)
D.
\(V=\frac{\pi(e-1)}{2}\)
Câu 27
Tất cả các giá trị của m để hàm số \(y=\frac{2 \cos x-1}{\cos x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là
A.
\(m>\frac{1}{2}\)
B.
\(m \geq \frac{1}{2}\)
C.
\(m>1\)
D.
\(m \geq 1\)
Câu 28
Cho hàm số y =f(x) có đồ thị như sau
A.
2
B.
4
C.
3
D.
1
Câu 29
COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới virus corona (nCOV) bắt đầu từ Trung Quốc (đầu tháng 12/2019) gây ra với tốc độ truyền bệnh rất nhanh (tính đến ngày 02/06/2020 đã có 6.365.173 người nhiễm bệnh. Giả sử ban đầu có 1 người nhiễm bệnh và cứ sau 1 ngày sẽ lây sang a người khác (\(a \in \mathbb{N}^{*}\) ). Tất cả những người nhiễm bệnh lại lây sang những người khác với tốc độ như trên (1 người lây cho a người). Tìm a biết sau 7 ngày có 16384 người mắc bệnh. (Giả sử người nhiễm bệnh không phát hiện bản thân bị bệnh, không phòng tránh cách ly và trong thời gian ủ bệnh vẫn lây sang người khác được)
A.
a=4
B.
a=2
C.
a=5
D.
a=3
Câu 30
Trong không gian Oxyz , cho điểm \(A(1 ;-3 ; 2)\) Tọa độ điểm A' đối xứng với A điểm qua mặt phẳng (Oyz) là
A.
\(A^{\prime}(0 ;-3 ; 2)\)
B.
\(A^{\prime}(-1 ;-3 ; 2)\)
C.
\(A^{\prime}(-1 ; 3 ;-2)\)
D.
\(A^{\prime}(-1 ; 3 ; 2)\)
Câu 31
Biết rằng hàm số \(y=f(x)=a x^{4}+b x^{2}+c\) có đồ thị là đường cong trong hình vẽ dưới đây.
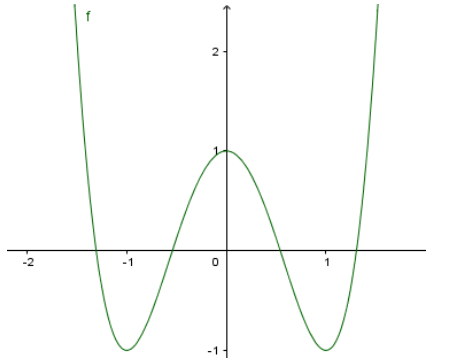

A.
1
B.
0
C.
-1
D.
-2
Câu 32
Tập nghiệm của bất phương trình \(\log _{2}^{2} x-5 \log _{2} x-6 \geq 0\) là:
A.
\(S=\left[\frac{1}{2} ; 64\right]\)
B.
\(S=[64 ;+\infty)\)
C.
\(S=\left(0 ; \frac{1}{2}\right]\)
D.
\(S=\left(0 ; \frac{1}{2}\right] \cup[64 ;+\infty)\)
Câu 33
Cho hình chóp \(S . A B C D\) có đáy là hình thoi cạnh a ,\(\widehat{ B A D}=60^{\circ},S B=S D=S C\) , M là trung điểm của SD , H là hình chiếu của S trên mặt phẳng (ABCD). Tính khoảng cách giữa hai đường thẳng SH và CM
A.
\(\frac{a \sqrt{17}}{14}\)
B.
\(\frac{a \sqrt{3}}{14}\)
C.
\(\frac{a \sqrt{7}}{7}\)
D.
\(\frac{a \sqrt{3}}{7}\)
Câu 34
Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;2;3) và song song với mặt phẳng \((P): x-2 y+z-3=0\) có phương trình là
A.
\(x-2 y+z-3=0\)
B.
\(x-2 y+z+3=0\)
C.
\(x-2 y+z=0\)
D.
\(x+2 y+3 z=0\)
Câu 35
Cho hàm số \(y=x^{3}-3 x^{2}+9\) có đồ thị là (C). Điểm cực tiểu của đồ thị (C) là
A.
\(M(0 ; 9)\)
B.
\(M(9 ; 0)\)
C.
\(M(5 ; 2)\)
D.
\(M(2 ; 5)\)
Câu 36
Trong không gian Oxyz cho mặt cầu (S) có tâm là I (0;0;1) và tiếp xúc với mặt phẳng \((\alpha): 2 x-2 y+z+8=0\) . Phương trình của (S ) là
A.
\(x^{2}+y^{2}+(z-1)^{2}=9\)
B.
\(x^{2}+y^{2}+(z+1)^{2}=9\)
C.
\(\begin{aligned}
&x^{2}+y^{2}+(z+1)^{2}=3
\end{aligned}\)
D.
\(x^{2}+y^{2}+(z+1)^{2}=3\)
Câu 37
Gọi Alà tập các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các số 1;2;3;4;5;6;7;8;9. Lấy ngẫu nhiên một số thuộc tập A. Tính xác suất để số lấy được luôn có mặt hai chữ số 1;2 và chúng không đứng cạnh nhau
A.
\(\frac{5}{36}\)
B.
\(\frac{1}{12}\)
C.
\(\frac{5}{12}\)
D.
\(\frac{1}{6}\)
Câu 38
Gọi\(z_1, z_2\) , là các nghiệm phức của phương trình\(z^{2}+z+1=0, \text { đặt } \mathrm{w}=z_{1}^{2021}+z_{2}^{2021}\)1 Khi đó
A.
\(\mathrm{w}=2^{2021}\)
B.
\(w=-1\)
C.
\(\mathbf{w}=2^{2021} i\)
D.
\(\mathbf{w}=1\)
Câu 39
Trong không gian Oxyz , phương trình mặt phẳng trung trực của đoạn thẳng AB với \(A(3 ;-2 ; 1) \text { và } B(1 ; 0 ; 5)\) là:
A.
\(x-y-2 z+3=0\)
B.
\(-2 x+2 y+4 z+3=0\)
C.
\(-2 x-2 y+4 z-6=0\)
D.
\(2 x-2 y-4 z-6=0\)
Câu 40
Cho đường thẳng \(d: \frac{x-2}{-1}=\frac{y+1}{-1}=\frac{z+1}{1}\)-và mặt phẳng \((P): 2 x+y-2 z=0\). Đường thẳng \(\Delta\) nằm trong (P), cắt d và vuông góc với d có phương trình là:
A.
\(\begin{aligned}
&\left\{\begin{array}{l}
x=1+t \\
y=-2 \\
z=t
\end{array}\right.
\end{aligned}\)
B.
\(\left\{\begin{array}{l}
x=1+t \\
y=-2 \\
z=-t
\end{array}\right.\)
C.
\(\begin{aligned}
&\left\{\begin{array}{l}
x=1-t \\
y=-2 \\
z=t
\end{array}\right.
\end{aligned}\)
D.
\(\left\{\begin{array}{l}
x=1-t \\
y=-2+t \\
z=-t
\end{array}\right.\)
Câu 41
Gọi F x ( ) là nguyên hàm của hàm số \(f(x)=\frac{x}{\sqrt{8-x^{2}}}\) thỏa mãn F(2)=0 . Khi đó phương trình F(x)=x có nghiệm là:
A.
\(x=1\)
B.
\(x=1-\sqrt{3}\)
C.
\(x=-1\)
D.
\(x=0\)
Câu 42
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a . Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2.HA . Cạnh SA hợp với mặt phẳng đáy góc \(60^0\) . Tính diện tích mặt cầu ngoại tiếp hình chóp S ABCD
A.
\(21 \pi a^{2}\)
B.
\(\frac{55 \pi a^{2}}{3}\)
C.
\(\frac{475 \pi a^{2}}{3}\)
D.
\(22 \pi a^{2}\)
Câu 43
Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số\(f x=m^{2}\left(\frac{e^{5 x}}{5}-16 e^{x}\right)+3 m\left(\frac{e^{3 x}}{3}-4 e^{x}\right)-14\left(\frac{e^{2 x}}{2}-2 e^{x}\right)+2020\) đồng biến trên \(\mathbb{R}\) . Tổng của tất cả các phần tử thuộc S bằng:
A.
\(-\frac{7}{8}\)
B.
\(\frac{1}{2}\)
C.
\( -2\)
D.
\(-\frac{3}{8}\)
Câu 44
Cho hàm số y=f(x) có đồ thị như hình sau:
A.
0
B.
1
C.
2
D.
-1
Câu 45
Cho hình chóp S .ABCD có đáy là hình thang vuông tại A và B , \(S A \perp(A B C D), A D=3 a\), \(S A=A B=B C=a\) . Gọi S ' là điểm thỏa mãn \(\overrightarrow{S S^{\prime}}=\frac{1}{2} \overrightarrow{A B}\). Tính thể tích khối đa diện \(S S^{\prime} A B C D\)
A.
\(\frac{13 a^{3}}{10}\)
B.
\(\frac{11 a^{3}}{12}\)
C.
\(\frac{11 a^{3}}{10}\)
D.
\(\frac{13 a^{3}}{12}\)
Câu 46
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
A.
5
B.
4
C.
6
D.
3
Câu 47
Cho x, y, zlà các số thực không âm thoả mãn \(12^{x}+2^{y}+2^{z}=10\) . Giá trị lớn nhất của biểu thức \(P=x+y+3 z\)gần nhất với số nào sau đây?
A.
8
B.
10
C.
9
D.
7
Câu 48
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) thỏa mãn \(f(x)=\left\{\begin{array}{ll}
x+m & \text { khi } x \geq 0 \\
c^{2 x} & \text { khi } x<0
\end{array}\right.\) (m là hằng số). Biết \(\int_{-1}^{2} f(x) \mathrm{d} x=a+b . c^{-2}\) . trong đó a b , là các số hữu tỷ. Tính a + b
A.
1
B.
4
C.
3
D.
0
Câu 49
Cho hàm số f x ( ) có bảng biến thiên như sau:
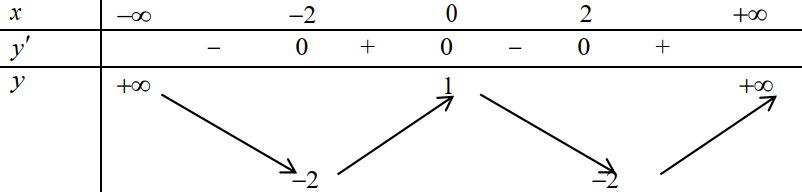
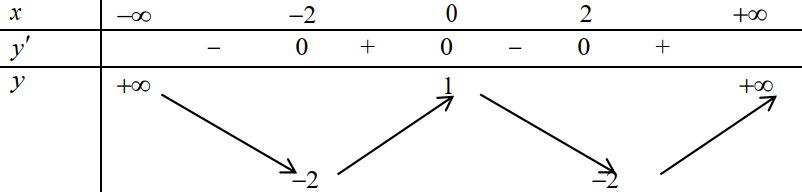
A.
\(\frac{575}{4}\)
B.
154
C.
156
D.
\(\frac{621}{4}\)
Câu 50
Cho Hàm số f(x) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số y =f'(x)như hình vẽ bên dưới
A.
1
B.
2
C.
0
D.
3