
ĐỀ THI Toán học
Ôn tập trắc nghiệm Hàm số lũy thừa Toán Lớp 12 Phần 5
Cho hai số thực x,y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaaqaba % GcdaqadaqaaiaadIhacqGHRaWkcaWG5bGaey4kaSIaaG4maaGaayjk % aiaawMcaaiabgwMiZkaaigdaaaa!47E5! {\log _{{x^2} + {y^2} + 2}}\left( {x + y + 3} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức S = 3x +4y -6.
Cho hai số thực x,y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikda % aaGccqGH+aGpcaaIXaaaaa!3C7A! {x^2} + {y^2} > 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaaIYaGaamyEamaaCaaameqabaGaaGOmaaaaaSqabaGcdaqada % qaaiaaikdacaWG4bGaey4kaSIaamyEaaGaayjkaiaawMcaaiabgwMi % Zkaaigdaaaa!4620! {\log _{{x^2} + 2{y^2}}}\left( {2x + y} \right) \ge 1\). Biết giá trị lớn nhất của P = x+y là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbGaey4kaSIaamOyamaakaaabaGaaGOnaaWcbeaaaOqaaiaadoga % aaaaaa!3A80! \frac{{a + b\sqrt 6 }}{c}\) với a,b,c là các số nguyên dương và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbaabaGaam4yaaaaaaa!37D2! \frac{a}{c}\) tối giản. Tính S = a+ b+ c
Số thực a nhỏ nhất để bất đẳng thức \(ln(1+x)\ge x - ax^2\) luôn đúng với mọi số thực dương x là \(\frac{m}{n}\) với m,n là các số nguyên dương và \(\frac{m}{n}\) tối giản. Tính
T = 2m+3n.
Tất cả các giá trị thực của m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaka % aabaGaamiEaaWcbeaakiabgUcaRmaakaaabaGaamiEaiabgUcaRiaa % igdacaaIYaaaleqaaOGaeyizImQaamyBaiaac6caciGGSbGaai4Bai % aacEgadaWgaaWcbaGaaGynaiabgkHiTmaakaaabaGaaGinaiabgkHi % TiaadIhaaWqabaaaleqaaOGaaG4maaaa!4807! x\sqrt x + \sqrt {x + 12} \le m.{\log _{5 - \sqrt {4 - x} }}3\) có nghiệm là
Trong tất cả các cặp (x;y) thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaaqaba % GcdaqadaqaaiaaisdacaWG4bGaey4kaSIaaGinaiaadMhacqGHsisl % caaI0aaacaGLOaGaayzkaaGaeyyzImRaaGymaaaa!496D! {\log _{{x^2} + {y^2} + 2}}\left( {4x + 4y - 4} \right) \ge 1\). Tìm m để tồn tại duy nhất cặp (x,y) sao cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikda % aaGccqGHRaWkcaaIYaGaamiEaiabgkHiTiaaikdacaWG5bGaey4kaS % IaaGOmaiabgkHiTiaad2gacqGH9aqpcaaIWaaaaa!4536! {x^2} + {y^2} + 2x - 2y + 2 - m = 0\).
Trong các nghiệm ( x ; y ) thỏa mãn bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaaIYaGaamyEamaaCaaameqabaGaaGOmaaaaaSqabaGccaGGOa % GaaGOmaiaadIhacqGHRaWkcaWG5bGaaiykaiabgwMiZkaaigdaaaa!45EF! {\log _{{x^2} + 2{y^2}}}(2x + y) \ge 1\). Giá trị lớn nhất của biểu thức T = 2x + y bằng:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIYaWaaWbaaSqabeaacaWG4bWaaWbaaWqabeaacaaIYaaaaSGaeyOe % I0IaaGinaaaakiabgkHiTiaaigdaaiaawIcacaGLPaaacaGGUaGaci % iBaiaac6gacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyipaWJaaGim % aaaa!43F9! \left( {{2^{{x^2} - 4}} - 1} \right).\ln {x^2} < 0\) là
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciyBaiaacg % gacaGG4bWaaiWaaeaaciGGSbGaai4BaiaacEgadaWgaaWcbaGaaG4m % aaqabaGccaWG4bGaai4oaiGacYgacaGGVbGaai4zamaaBaaaleaada % WcaaqaaiaaigdaaeaacaaIYaaaaaqabaGccaWG4baacaGL7bGaayzF % aaGaeyipaWJaaG4maaaa!47C3! \max \left\{ {{{\log }_3}x;{{\log }_{\frac{1}{2}}}x} \right\} < 3\) có tập nghiệm là.
Tìm tập xác định hàm số sau \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maakaaabaGaciiBaiaa % c+gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabe % aakmaalaaabaGaaG4maiabgkHiTiaaikdacaqG4bGaeyOeI0IaamiE % amaaCaaaleqabaGaaGOmaaaaaOqaaiaadIhacqGHRaWkcaaIXaaaaa % Wcbeaaaaa!47FA! f\left( x \right) = \sqrt {{{\log }_{\frac{1}{2}}}\frac{{3 - 2{\rm{x}} - {x^2}}}{{x + 1}}} \)
Gọi \(S_1,S_2,S_3\) lần lượt là tập nghiệm của các bất phương trình sau: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmamaaCa % aaleqabaGaamiEaaaakiabgUcaRiaaikdacaGGUaGaaG4mamaaCaaa % leqabaGaamiEaaaakiabgkHiTiaaiwdadaahaaWcbeqaaiaadIhaaa % GccqGHRaWkcaaIZaGaeyOpa4JaaGimaaaa!4265! {2^x} + {2.3^x} - {5^x} + 3 > 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWG4bGaey4k % aSIaaGOmaaGaayjkaiaawMcaaiabgsMiJkabgkHiTiaaikdaaaa!4137! ;{\log _2}\left( {x + 2} \right) \le - 2\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaada % WcaaqaaiaaigdaaeaadaGcaaqaaiaaiwdaaSqabaGccqGHsislcaaI % XaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaamiEaaaakiabg6da+i % aaigdaaaa!3DCA! ; {\left( {\frac{1}{{\sqrt 5 - 1}}} \right)^x} > 1\).Tìm khẳng định đúng?
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWadaqaamaabmaabaGaamiEaiabgUcaRiaaigdaaiaawIcacaGL % PaaadaqadaqaaiaadIhacqGHsislcaaIYaaacaGLOaGaayzkaaWaae % WaaeaacaWG4bGaeyOeI0IaaG4maaGaayjkaiaawMcaaiabgUcaRiaa % igdaaiaawUfacaGLDbaacqGH+aGpcaaIWaaaaa!49AB! \ln \left[ {\left( {x + 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\) là
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWadaqaamaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGL % PaaadaqadaqaaiaadIhacqGHsislcaaIYaaacaGLOaGaayzkaaWaae % WaaeaacaWG4bGaeyOeI0IaaG4maaGaayjkaiaawMcaaiabgUcaRiaa % igdaaiaawUfacaGLDbaacqGH+aGpcaaIWaaaaa!49B6! \ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\) là
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaalaaabaGaamiEaiabgUcaRiaaikdaaeaacaaIZaGaeyOeI0IaaG % OmaiaadIhaaaGaeyyzImRaaGimaaaa!430F! {\log _{\frac{1}{2}}}\frac{{x + 2}}{{3 - 2x}} \ge 0\) là
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iGacYgacaGGVbGaai4z % amaaBaaaleaadaWcaaqaaiaaigdaaeaacaaIZaaaaaqabaGcdaqada % qaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI1aGaamiE % aiabgUcaRiaaiEdaaiaawIcacaGLPaaaaaa!46BE! f\left( x \right) = {\log _{\frac{1}{3}}}\left( {{x^2} - 5x + 7} \right)\). Nghiệm của bất phương trình f(x) > 0 là:
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOGaamiEaiabgUcaRiGacYga % caGGVbGaai4zamaaBaaaleaacaaIZaaabeaakiaadIhacqGH+aGpca % aIXaaaaa!4217! {\log _2}x + {\log _3}x > 1\) có nghiệm là
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaiodaaeqaaO % WaaSaaaeaacaaIYaGaamiEaiabgUcaRiaaigdaaeaacaWG4bGaeyOe % I0IaaGymaaaaaiaawIcacaGLPaaacqGH+aGpcaaIWaaaaa!479A! {\log _{\frac{1}{2}}}\left( {{{\log }_3}\frac{{2x + 1}}{{x - 1}}} \right) > 0\) có tập nghiệm là
Tập nghiệm của bất phương trình: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaiodaaaaabeaa % kmaabmaabaGaamiEaiabgkHiTiaaiodaaiaawIcacaGLPaaacqGHsi % slcaaIXaGaeyOpa4JaaGimaaaa!421C! {\log _{\frac{1}{3}}}\left( {x - 3} \right) - 1 > 0\) có dạng (a;b). Khi đó giá trị a + 3b bằng ?
Tậpnghiệmcủabấtphươngtrình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaiAdaaeqaaO % WaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamiE % aaqaaiaadIhacqGHRaWkcaaI0aaaaaGaayjkaiaawMcaaiabgYda8i % {\log _{\frac{1}{2}}}\left( {{{\log }_6}\frac{{{x^2} + x}}{{x + 4}}} \right) < 0\) là
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaeWaaeaaciGGSbGaai4B % aiaacEgadaWgaaWcbaWaaSaaaeaacaaIXaaabaGaaGOmaaaaaeqaaO % GaamiEaaGaayjkaiaawMcaaiabgYda8iaaigdaaaa!4289! {\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\) là:
Tìm tất cả giá trị thực của tham số m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaeWaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaey4kaSIaaGinaiaadIhacqGHRaWkcaWGTb % aacaGLOaGaayzkaaGaeyyzImRaaGymaaaa!4421! {\log _3}\left( {{x^2} + 4x + m} \right) \ge 1\) nghiệm đúng với mọi ?
Tìm tất cả các giá trị thực của tham số m để phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWGTbGaamiE % aiabgkHiTiaadIhadaahaaWcbeqaaiaaikdaaaaakiaawIcacaGLPa % aacqGH9aqpcaaIYaaaaa!41CD! {\log _2}\left( {mx - {x^2}} \right) = 2\) vô nghiệm?
Tìm tất cả các giá trị thực của tham số m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOGaaiikaiaaiwdadaahaaWc % beqaaiaadIhaaaGccqGHsislcaaIXaGaaiykaiabgsMiJkaad2gaaa % a!4151! {\log _2}({5^x} - 1) \le m\) có nghiệm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgw % MiZkaaigdaaaa!3972! x \ge 1\) ?
Điều kiện xác định của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaai4BaiaacE % gadaWgaaWcbaWaaSaaaeaacaaIXaaabaGaaGOmaaaaaeqaaOWaamWa % aeaaciGGSbGaai4BaiaacEgadaWgaaWcbaGaaGOmaaqabaGccaGGOa % GaaGOmaiabgkHiTiaadIhadaahaaWcbeqaaiaaikdaaaGccaGGPaaa % caGLBbGaayzxaaGaeyOpa4JaaGimaaaa!45F7! lo{g_{\frac{1}{2}}}\left[ {{{\log }_2}(2 - {x^2})} \right] > 0\) là:
Điều kiện xác định của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWcaaqaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI % XaaabaGaamiEaaaacqGH8aapcaaIWaaaaa!3E3B! \ln \frac{{{x^2} - 1}}{x} < 0\)
Tìm số nghiệm nguyên của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaakaaabaGaaG4maaadbeaaliabgkHiTiaa % igdaaeqaaOWaaeWaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey % OeI0IaaGOmaiaadIhacqGHRaWkcaaIXaaacaGLOaGaayzkaaGaeyOp % a4JaaGimaiaac6caaaa!45B6! {\log _{\sqrt 3 - 1}}\left( {{x^2} - 2x + 1} \right) > 0.\)
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaai4BaiaacE % gadaWgaaWcbaGaaGOmaaqabaGccaGGOaGaamiEamaaCaaaleqabaGa % aGOmaaaakiabgkHiTiaaiodacaWG4bGaey4kaSIaaGymaiaacMcacq % GHKjYOcaaIWaaaaa!42C0! lo{g_2}({x^2} - 3x + 1) \le 0\) là ;
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaikdaaeqaaO % WaaeWaaeaacaaIYaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPaaa % aiaawIcacaGLPaaacqGH+aGpcaaIWaaaaa!4678! {\log _{\frac{1}{2}}}\left( {{{\log }_2}\left( {2x - 1} \right)} \right) > 0\) là:
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGOmaaqaaiaaiodaaaaabeaa % kmaabmaabaGaaGOmaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsi % slcaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaaiabgYda8iaaicda % aaa!43FC! {\log _{\frac{2}{3}}}\left( {2{x^2} - x + 1} \right) < 0\) có tập nghiệm là:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaSaaaeaacaaI0aGaamiE % aiabgUcaRiaaiAdaaeaacaWG4baaaiabgsMiJkaaicdaaaa!408F! {\log _3}\frac{{4x + 6}}{x} \le 0\) là:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPaaacqGHLj % YScaaIWaaaaa!412E! {\log _{\frac{1}{2}}}\left( {x - 1} \right) \ge 0\) là:
Tìm tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaio % dacaWG4bGaey4kaSIaaGOmaaGaayjkaiaawMcaaiabgwMiZkabgkHi % Tiaaigdaaaa!45AC! {\log _{\frac{1}{2}}}\left( {{x^2} - 3x + 2} \right) \ge - 1\)
Tìm tập nghiệm S của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaalaaabaGaaGOmaaqaaiaadIhacqGHsislcaaIXaaaaiabg6da+i % aaikdaaaa!3FB6! {\log _{\frac{1}{2}}}\frac{2}{{x - 1}} > 2\)
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHLjYScqGHsislcaaIXa % aaaa!3FDF! {\log _{\frac{1}{2}}}{x^2} \ge - 1\) là
Tìm tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaicdacaGGSaGaaGynaaqabaGcdaqadeqa % aiaaikdacaWG4bGaeyOeI0IaaGymaaGaayjkaiaawMcaaiabg6da+i % abgkHiTiaaikdaaaa!42BF! {\log _{0,5}}\left( {2x - 1} \right) > - 2\)
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiabgY % da8iGacYgacaGGVbGaai4zamaaBaaaleaacaaIYaaabeaakiaadIha % cqGH8aapcaaI0aaaaa!3E35! 3 < {\log _2}x < 4\) là:
Giải bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaG4maaqaaiaaisdaaaaabeaa % kmaabmaabaaeaaaaaaaaa8qacaaIYaGaamiEaiabgkHiTiaaigdaa8 % aacaGLOaGaayzkaaWdbiabg6da+iaaikdaaaa!4171! {\log _{\frac{3}{4}}}\left( {2x - 1} \right) > 2\) ta được:
Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {2x - 1} \right) > - 1\) là:
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaaGOmaiaadIhacqGHRaWkcaaIZa % aacaGLOaGaayzkaaGaeyOpa4JaaGymaaaa!4337! {\log _2}\left( {{x^2} - 2x + 3} \right) > 1\) có tập nghiệm là
Tìm tọa độ giao điểm M của hai đồ thị hàm số \(y = 3^x\) và \(y = \frac{1}{3}\).
Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
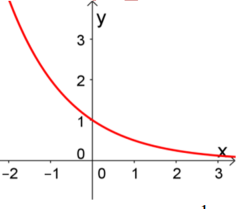
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
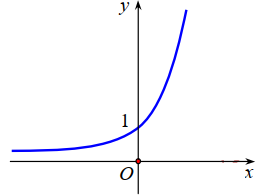
Hàm số nào trong các hàm số dưới đây có đồ thị phù hợp với hình vẽ bên?
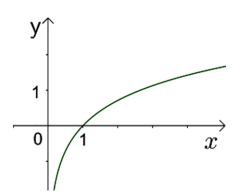
Cho \( \alpha, \beta \) là các số thực. Đồ thị các hàm số \(y = x^{\alpha} , y = x^{\beta}\)trên khoảng \((0; +\infty)\) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
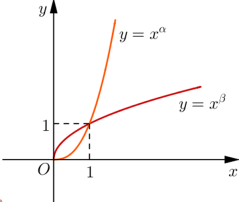
Cho hàm số \(y=x^{-\sqrt2}\) . Mệnh đề nào sau đây là sai?
Cho hàm số \(y = x^{e-3}\)trong các kết luận sau kết luận nào sai?
Cho hàm số \(y = x^ {-\sqrt{2017}}\) . Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số
Hình vẽ bên là đồ thị các hàm số \(y = x^a , y = x^b , y = x^c\) trên miền \((0;+\infty)\) . Hỏi trong các số a, b, c số nào nhận giá trị trong khoảng (0; 1) ?
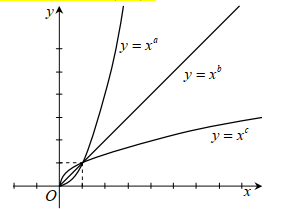
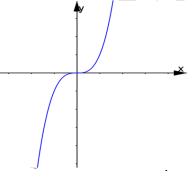
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên
Tính đạo hàm của hàm số \(y = log (ln 2x)\)
Cho hàm số \(f (x) = ln (x⁴ +1)\) . Đạo hàm f'(1) bằng